Spatial Organization Compartments (SOC) scheduling

SOC and spatial harvest planning

A SOC (Spatial Organization Compartment) is a forest area that can be used to spatially aggregate harvest areas. In Woodstock, it is represented in a spatially referenced way by a group of areas or stands that share a common SOC number.

The aggregation of harvest areas was for a time frowned upon in some countries because of the large areas of continuous cut forest it could generate. However, it is now being reconsidered with the aim of minimizing the extent of cut areas on the landscape, as well as the amount of logging roads generated. The cost of cutting is also reduced by reducing travel and complexity during forestry operations.

FMT thus provides various functions that allow deriving a SOC opening and closing schedule that respects several given spatial constraints on the size of the cut areas. Thus, the schedule will close SOCs that are too close together when this could cause cut sizes to be too large if selected, or force large cuts by restricting the SOCs available for cutting.

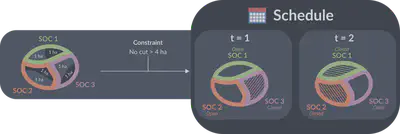
This SOC opening and closing schedule will thus allow to communicate spatial constraints to the linear programming models based on the Woodstock files that FMT uses (see FMT basics). FMT will then be able to generate a new solution for a model with the addition of this calendar. Of course, when additional constraints are added to the model, it usually reduces the amount of wood that can be harvested in the optimal solution. Thus, adding this schedule of SOC openings and closings will reduce the amount of wood harvested in the new solution generated by FMT.

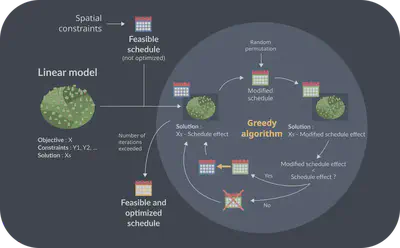
The idea is then to find an “optimal” schedule that will reduce the amount of harvestable wood in the model solution as little as possible. This can be done through the following iterative process:

• Compute the model solution without a schedule.
• A first schedule of SOC opening and closing is generated that respects the given spatial constraints.
  • This schedule is simply “feasible”; it is not necessarily optimized, but simply respects all constraints.
• The schedule is added to the model, and the model solution is recalculated.
• We compare the amount of wood harvested in the first solution (without schedule) with this new solution (with schedule). We obtain the % reduction of harvestable wood for which the schedule is responsible.
  • The goal is then to optimize the schedule to reduce this percentage as much as possible.
• We then perform the following loop (called a greedy algorithm) with as many iterations as necessary:
  • We change the SOC schedule randomly while ensuring that it continues to meet all spatial constraints
  • We insert the schedule into the model and recalculate the solution
  • If the schedule has reduced the percentage reduction in harvestable timber, the random change is saved for the next iteration
    • If not, we cancel this random modification and look for another one

The implementation of SOC in Woodstock files

The syntax of Woodstock files is not designed to allow optimization via spatial constraints. However, the SOC system used by FMT can be implemented in Woodstock files through a yield.

For example, it is possible to create a yield named yopen that describes whether a stand is available for harvest or not. This yield can then be assigned to a SOC number in a theme, and will therefore apply to all stands that are associated with that SOC number via that same theme. It can then be used to restrict certain actions (e.g., cuts) within the model.

In the YIELD section of the woodstock model, this yield which indicates when a SOC is open or closed will have a value for each period of the model. This sequence of values thus represents the opening or closing schedule of the SOC. In practice, the YIELD section which contains the schedule formulated by FMT will take the following form (here, the yield yield indicates whether a SOC is open or closed):

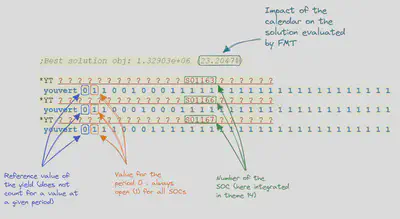
With respect to an action in the model such as a cut, the yield can be used in the ACTION section of the model to restrict the action to open SOC as follows:

Functions used and required parameters

FMT offers several functions that allow to create an optimized SOC opening and closing schedule in FMT. These functions require different parameters that will be described here.

Creating SOC within a linear programming model in FMT

In FMT, once a linear model has been created based on woodstock files (see FMT basics), it is possible to create the structure of SOCs within the model (see previous sections) through the Heuristics.FMToperatingareascheme() function.

The function Heuristics.FMToperatingareascheme() is used to build a single SOC within the model, and therefore must be repeated for each SOC that is to be created. It requires different parameters. These parameters are used to give constraints on how and when a SOC can be opened in the calendar.

You will find an example of this creation in the next section.

• The first parameter contains the SOC to create itself. It can be constructed using the function Heuristics.FMToperatingarea(), which itself takes two parameters: the first is the mask that will describe which stands will be contained in this SOC, and the second is the neihgbors perimeter. This second parameter describes the ratio of the perimeter of the SOC that it must have in common with another SOC for both to be considered neighbors. For example, if the neighbor perimeter is 0.5, then 50% of the SOC perimeter must be shared with another SOC for them to be considered neighbors.
• The second parameter is the opening time. It defines how long the SOC should remain open when it is open for a period of time. For example, if the opening time is 5, then the SOC will always be open for 5 periods at a time.
• The third parameter is the return time. This is the number of periods of time that must be met before the SOC is reopened in the future. For example, if the return time is 5, then there must be at least 5 time periods between two openings of the SOC.
• The fourth parameter is the repetition pattern, or the repetition of the harvest pattern. It is greater than or equal to 1, and it will effectively force the SOC to follow a pattern of openings/closures several times in time that corresponds to an alternation between its opening and closing time. For example, for an opening time of 2, a closing time of 3 and a harvest pattern repetition value of 2, once the SOC is opened, it will automatically follow the “open, open, closed, closed, open, closed, closed” schedule, which corresponds to 2 repetitions of its opening and closing parameters.
• The fifth parameter is the green up period. It corresponds to the time the SOC has to wait to be opened again if a neighboring SOC is harvested. Neighboring SOC are in turn found through the perimeter of the neighbors given earlier.
• The sixth parameter is the starting period. It corresponds to the period from which the SOC can start to be opened in the model.

All SOC created by the function Heuristics.FMToperatingareascheme() should ideally be put into a list, which will be given as parameter to another function later.

Determining neighboring SOCs to use advanced spatial constraints

You may have a shapefile containing the spatial position of each of the SOC.

If this is the case, then it is possible to determine which SOC are neighbors by reading the shapefile, and comparing the polygon numbers corresponding to the SOC in the shapefile with those in the linear model files. This makes it possible to use the spatial constraint determined by the green up period parameter described in the previous section.

This can be done by using the getschemeneighbors() function of a previously created FMTareaparser object, and providing it with the list of SOC created through Heuristics.FMToperatingareascheme() (see previous section) as well as the shapefile (or other type of vector file) that contains the SOC. Then you just have to indicate which fields of the shapefile contain the information related to the age of the SOC and their area. It is possible to use optional parameters in order not to consider SOC with too small areas.

In doing so, the getschemeneighbors() function will return a list of SOCs similar to that created by Heuristics.FMToperatingareascheme(); however, for each of the SOCs, the vector indicating the list of their spatial neighbors will be filled in.

This should take the following form:

# We create the FMTareaparser object to read the files
areap = Parser.FMTareaparser()
# We indicate the location of the shapefile
shapefileLocation = "./spatialCompartments.shp"
# We use the function on a list of SOC already created with Heuristics.FMToperatingareascheme() before, operaeas
# The "modelthemes" object contains the themes of the model
# The list will be updated with SOC that contain their neighbors vector filled according to their position in space described in the vector file spatialCompartments.shp given as argument
opeareas = areap.getschemeneighbors(opeareas,modelthemes,shapefileLocation,"AGE","SUPERFICIE")

For more information, see the doxygen page of FMTareaparser and the section on getschemeneighbors

Creation of an output node related to actions influenced by the SOC schedule.

In order to start optimizing the SOC schedule (see next section), we need to provide FMT with different information when it comes to the actions and stands that will be affected by the SOC. To do this, FMT needs a FMToutputnode object related to the actions that will be targeted by the SOC openings and closings (e.g., a type of cutting that cannot be done too close to each other). These objects are only used because they are the most useful for this step, not because they are the only ones that can give this information to FMT.

The FMToutputnode objects contain the output nodes of the linear model. These are composed of 4 elements: a mask (to define the stands considered by the output node), an action, a yield, and a parameter that can be used to modify the yield. For example, an output node can concern 80% of the gross volume harvested by total cuts in all stands via the statement ? ? ? coupetotale volumebrut * 0.88. The output nodes are indicated in the .out file of the Woodstock formulation. Several output nodes can then be combined to give a single output.

In order to provide these FMToutputnode to FMT, two methods are available:

1. It is possible to create a new FMToutputnode object that will contain all the actions targeted by the SOC by making an aggregate of these actions. To do this, you just have to give an aggregate name to all the actions via the push_aggregate() function associated to the FMTaction objects; then, to give this aggregate name to the FMToutputnode constructor. If these actions concern all possible stands, then the constructor to take the form FMToutputnode(Core.FMTmask("? "*len(themes))[:-1],themes),Agg_name), with Agg_name containing the name of the aggregate of actions targeted by the SOC.
2. It is also possible to retrieve an FMToutputnode that is contained in one of the FMToutput of the model directly via the getnodes() function associated with the FMToutput objects.

An example of the second method is shown in sample script below.

Launching the greedy algorithm and retrieving the optimized calendar

The last step is to launch the greedy algorithm to create an optimized calendar.

To do this, you just have to create an object that will contain the greedy algorithm’s “task”, and to give this task to a function of FMT that will launch the parallel tasks. These two steps are essential, because the greedy algorithm of FMT uses parallel tasks in order to perform the different iterations of the algorithm as quickly as possible.

The creation of the object containing the algorithm’s task is done via the function Parallel.FMTopareaschedulertask(). The function requires 7 parameters:

• The FMTlpmodel which contains the linear model for which we want to do the SOC schedule
• An object containing the list of SOC (see previous section)
• The output node created in the previous section
• A string (string) that indicates where the files created by the function (that contain information about the final optimized calendar) will be copied
• A string (string) indicating the name of the output related to the open or closed status of the SOC (e.g. yopen; see previous sections)
• A number indicating the maximum number of iterations the greedy algorithm can perform before stopping (see previous sections)
• A number indicating the maximum time (in seconds) the greedy algorithm can take before stopping; the algorithm will stop if this time or the maximum number of iterations is reached

Once the object containing the task is created with this function, it must be passed to the function Parallel.FMTtaskhandler(). This function can accept a second parameter that specifies the number of cores in the computer’s processor that the function will use to perform the parallel operations. The function will return an FMTtaskhandler object, which can then run the algorithm in earnest using the object’s concurentrun() function.

It is also possible not to run the greedy algorithm, but simply to obtain a first non-optimized and “feasible” schedule. To do this, one just has to use the getoperatingareaschedulerheuristics() function of an FMTlpmodel object by providing it with an object containing the list of SOC and an output node, as well as the number of non-optimized schedules one wants to obtain. An example is shown in this script on lines 34-35.

Example script

A very simple sample script to create a non-optimized SOC calendar in python is available at this address. This script only generates an initial unoptimized version of a SOC calendar, but one that is simply feasible within the constraints given.

The following script is another version of this script which is fully commented, and which runs at the end the greedy algorithm to get an optimized SOC schedule.

# Ici, on charge FMT directement, comme si il avait été installé avec pip.
from FMT import Models
from FMT import Parser
from FMT import Core
from FMT import Heuristics
from FMT import Version                  


if __name__ == "__main__":
	# We check that FMT has the necessary functions for this script
	if Version.FMTversion().hasfeature("OSI"):
		# Defining the path leading to the woodstock model files
		primarylocation = "../Models/TWD_land/TWD_land.pri"
		# Creatomg an object to read the model (parser)
		modelparser = Parser.FMTmodelparser()
		# Reading the model using the parser
		models = modelparser.readproject(primarylocation,["LP"])
		# Disabling logging for this model (optional)
		models[0].setquietlogger()
		# Loading the model in the list of models returned
		optimizationmodel=Models.FMTlpmodel(models[0],Models.FMTsolverinterface.CLP)
		# Gathering the themes of the model
		themes = optimizationmodel.getthemes()
		# Creating a list to fill with the operating areas
		opareas = []
		# For each of the SOC numbers present in the themes, we create a SOC that we put in the list
		for attribute in themes[2].getattributes("?"):
			mask = ["?" for theme in themes]
			mask[2] = attribute
			# We create the SOC with the mask that selects the forest stands with the number of the SOC
			# We use an opening time of 2, a return time of 1, a reptition of 4, a green up period of 0, and a starting period of 1.
			opareas.append(Heuristics.FMToperatingareascheme(Heuristics.FMToperatingarea(Core.FMTmask(mask,themes),0),2,1,4,0,1))
		# The following lines are used to find an initial solution to the model, without any SOC schedule. See the Basics of FMT section.
		for period in range(0,10):
				print(optimizationmodel.buildperiod())
		allconstraints = optimizationmodel.getconstraints()
		objective = allconstraints.pop(0)
		for constraint in allconstraints:
				optimizationmodel.setconstraint(constraint)
		optimizationmodel.setobjective(objective)
		optimizationmodel.initialsolve()
		# We gather the output nodes of the model necessary to create the SOC schedule via the actions that they contain
		nodeofoutput = None
		for output in optimizationmodel.getoutputs():
				if "OSUPREC" == output.getname():
					  nodeofoutput = output.getnodes(optimizationmodel.getarea(),optimizationmodel.getactions(),optimizationmodel.getyields())[0]
					  break;
		# We finish by defining the necessary parameters to launch the greedy algorithm : the location of the outputs, the maximal time and maximal number of iterations for the algorithm
		outputsLocation = "./Outputs/outputCalendrier"
		maximumIterations = 30
		maximumTime = 1209600 # Maximum time in seconds; here, it corresponds to two weeks.
		# We create the object that will contain the task to launch with the greedy algorithm
        maintask = Parallel.FMTopareaschedulertask(optimizationmodel, opeareas, outputsLocation, "YOUVERT", maximumIterations, maximumTime)
        # We put the task inside an object that deals with launching parralel tasks in FMT
        handler = Parallel.FMTtaskhandler(maintask,self.thr)
        # We active the log during the parallel tasks
        handler.settasklogger()
        # We launch the task of the greedy algorithm in parallel
        handler.conccurentrun()
	else:
		print("FMT needs to be compiled with OSI")