Spatially referenced re-planning

What is re-planning?

Re-planning is a process that consists of re-solving a forest planning optimization model (such as those used in FMT) to take into account elements that cannot be considered in the traditional process of solving these models.

Re-planning therefore allows for more complex questions to be asked; in particular, it allows for interactions between the different levels of hierarchical planning in forestry (strategic, tactical and operational).

Here are some examples of questions that re-planning can answer :

• Questions related to the effects of natural disturbances (fire, spruce budworm, etc.)
  • What is the effect of fire on the determination of harvest levels by the strategic model ?
  • What is the effect of a change in stochastic (random) disturbance regime on the determination of harvest levels by the strategic model ?
• Questions related to inconsistencies between what is planned at the strategic (large-scale) level, and the reality on the ground (small-scale): this is the notion of drift between different levels of hierarchical management
  • Are the objectives always achieved by taking into account more precise problems and constraints at tactical level ?
• Questions related to interactions between the strategic and tactical levels
  • What is the effect of communicating (or not) certain information to the tactical or strategic model? What changes? What does not change ?

Spatially referenced re-planning in practice

Models used

When using FMT, spatially referenced re-planning is in practice done by using 3 different FMT models.

These 3 models represent 3 scenarios applied to the same initial landscape (same sections AREA, CONSTANTS, LANDSCAPE, OUTPUTS). However, these scenarios can have different elements from each other (different ACTIONS, TRANSITIONS, YIELDS and OPTIMIZE sections).

These three models are :

1. The strategic model

This is a type III linear programming model, as described in FMT basics.

This is the model that will represent what happens at the strategic level, i.e. when we look at things from above without taking into account certain details at finer scales.

2. The stochastic model

It is a non-spatial simulation model (which works in a spatially referenced space like the linear models, and not a spatially explicit space).

It will be used to simulate pseudo-random actions with area targets to be reached. These actions can represent forest fires, insect epidemics, and many others!

3. The tactical model

Like the strategic model, this is a type III linear programming model, as described in FMT basics.

This model will be used to redo an optimization of the forest planning while taking into account the changes that the stochastic model may have made on the landscape, or with different or additional constraints compared to the strategic model.

The example of a re-planning iteration

Re-planning is done using the three models described above, calling them one after the other within each re-planning period. As one of the models (the stochastic model) contains random events, it is however possible to re-do the whole process several times in order to take into account the variability linked to these random events: this is called an iteration.

When the models are called one after the other, some of their characteristics are passed from one to the other (inventory/state of the landscape for the period, or constraints and existing planning).

In the end, a re-planning iteration takes the following form:

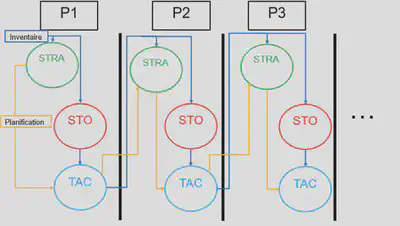
In this diagram,

• STRA corresponds to the strategic model
• STO corresponds to the stochastic model
• TAC corresponds to the tactical model

We can thus see that for each period,

• The strategic model is called to do its planning.
  • The planning of the strategic model is done on a long time horizon; and this horizon does not change through the periods. That is to say that at each period, the strategic model will, for example, plan for the next 100 years; whether it is 100 years after period 1, or 100 years after period 3.
• The strategic model share it’s inventory with the stochastic model, which is called to do its simulation.
  • The stochastic model will only do this simulation for the given period of time (contrary to the planning model which will do its optimization by taking into account a long time horizon). This is because the stochastic model only simulates random events, and does not try to optimize anything.
• The inventory resulting from the stochastic model will be passed to the tactical model, which is called to do its re-planning.
  • The tactical model will only plan for the given time period; it will not simulate the long term like the strategic model, although it will do optimization and not simulation. Its objective will be, for example, to harvest wood without exceeding the amount of wood harvested by the strategic model, but by taking into account the inventory modified by the random events of the stochastic model.
• The inventory resulting from the tactical model is then passed back to the strategic model, which will then plan again for the next period.

We can thus see two back and forth between the models:

• The transition of the inventory from one model to another as the process proceeds (blue lines on the diagram)
• The passage of planning constraints from the strategic model to the tactical model (yellow lines on the diagram)

Note that this whole process is only one iteration of re-planning. In order to really take into account the effects of stochastic events in the stochastic model, it is important to repeat this whole process many times. This allows to take into account the variability that will exist in how the inventory and tactical model will react to random events; the tactical model may also contain random components within it.

The re-planning models in detail

The strategic model

• It is a linear programming optimization model (FMTlpmodel).
  • It does not take into account natural disturbances or stochastic events.
• Normally, it has a long planning horizon for long-term optimization (e.g. 100 to 150 years).
• It dictates the path to take to the tactical model by sharing informations with it.
• It can use the new keyword _SETFROMLOCAL(ratio).

The stochastic model

• It is a non-spatial simulation model (FMTnssmodel).
  • It simulates natural disturbances or stochastic events.
• It may have a long simulation horizon; but it simulates only one period at a time.
• Its role is to affect the territory used by the tactical model, and thus to blur the lines between the strategic model and the tactical model.
• It can use the new keywords _RANDOM(output) and _REPLICATE(output).

The tactical model

• It is a linear programming optimization model (FMTlpmodel), like the strategic model.
• Its planning horizon is only one period.
  • Because at the tactical level, we only take into account the short-term, and not the long-term.
• Its initial state is that of the current period, given by the stochastic-model.
• It can use the new keywords _SETFROMGLOBAL(ratio) and _SETGLOBALSCHEDULE(ratio).

The new keywords associated with re-planning

Different keywords that do not exist in the Woodstock syntax allow the implementation of back and forth information between the different models of re-planning, according to the following scheme:

Others allow you to ignore constraints at given times, or to adjust them.

You will find here the list of these new keywords related to re-planning:

_REIGNORE(period)

This keyword must appear in the OPTIMIZE section of a model.

It informs the model to ignore a constraint from a specific re-planning period.

This can be very useful to set up a period for re-planning, and then ignore the related constraints.

_REPLICATE(output)

This keyword allows you to change the right-hand side of the equation (Right Hand Side, or RHS) of a constraint by fetching a value from an array containing these values for different replicates.

In practice, you can put a .csv file in the scenario directory, and then use _REPLICATE(csv file) to make FMT apply a certain value in that array for the current iteration.

For example, writting the following in the constraints section of a model:

_RANDOM(outputaction) <= 10 1 _REPLICATE(file.csv)

replaces, for each iteration, the number “10” in the constraint with the number in line 1 of the file file.csv with the column that corresponds to the iteration.

In the file, the rows correspond to the period and the columns to the iteration to which we want the value to apply.

_SETFROMLOCAL(ratio)

This keyword allows the strategic model to adjust one of its constraints according to the corresponding output value in the tactical model used at the previous period.

With this constraint, we specify a ratio that can increase or decrease the value taken from the tactical-model. For example, a ratio of 1.0 will give exactly the value of the tactical model; a ratio of 2.0 will multiply it by two, and a ratio of 0.5 will divide it by two.

If we write the following in the constraints section of a strategic model:

VOLUMEREC <= 0 1.._LENGTH _SETFROMLOCAL(1)

the “0” of the RHS is systematically replaced by the value of the VOLUMEREC output of the previous re-planning period of the tactical model.

_RANDOM(output)

This keyword is used to generate random values for the stochastic model.

It is written as a standard constraint.

Here is an example to generate a random number between 50 and 100 for period 1 to LENGTH:

_RANDOM(outputaction) <= 50 1.._LENGTH
_RANDOM(outputaction) >= 100 1.._LENGTH

_SETFROMGLOBAL(ratio)

This keyword is used to adjust a constraint of the tactical model based on a value determined by the strategic model. It is somewhat the reciprocal of _SETFROMLOCAL(ratio).

The ratio allows to increase or decrease the value taken from the strategic model. For example, a ratio of 1.0 will give exactly the value of the strategic model; a ratio of 2.0 will multiply it by two, and a ratio of 0.5 will divide it by two.

If we write the following in the constraints section of a tactical model:

VOLUMEREC <= 0 1.._LENGTH _SETFROMGLOBAL(1)

the number “0” of the RHS is systematically replaced by the value of the VOLUMEREC output of the strategic model for the current re-planning period.

_SETGLOBALSCHEDULE(ratio)

This keyword makes it possible to include the solution (what has been planned as actions) of the strategic model in the tactical model as a weight to the objective function.

To do so, when evaluating the solution of the tactical model, each time the latter plans an action on the same development as provided for in the strategic model, it will multiply the planned area (at the tactical level) by the specified ratio and add value to the objective according to the formulation of the objective function. If the model is to maximize, we will add up and if it is to minimize, we will subtract the calculated value.

The results of the re-planning

As a result of the re-planning process, the following results are obtained:

• Three raw results files (one per model)
• One probability file (one for the whole process)

Raw results files by model

These files contain values related to the outputs in the different models, for the different periods, and for the different iterations.

They contain different columns:

• Iteration: Indicates the number of the iteration used to take stochasticity into account. Iteration “0” is for the “base” strategy model, which is resolved at the very beginning of the re-planning process.
• Period: Indicates the period of re-planning that concerns the value of the output.
• Output: Name of the output being considered.
• Value: Value of the output under consideration.
• Type: Type of output (indicates whether it is a “total” output for the entire landscape, or per development/settlement).

The probability file

This file contains the probability that outputs of the tactical model may drift from the solution of the initial strategic model (solved at the very beginning of the re-planning process), whose outputs are in the “0” iteration of the raw results files.

For each of the outputs defined in the models, the probability file will contain all the probabilities of staying in the lower and upper range of the distance ratio (drift) to the outputs of the [strategic model](. /#the-strategic-model), for the following drift values: 0, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50.

This file contains different columns:

• Period: Indicates the period of rescheduling that concerns the value of the output.
• Output: Name of the output considered.
• LowerProbability: Probability of staying in the lower range of the distance ratio.
• UpperProbability: Probability of remaining in the upper range of the distance ratio.
• Drift: Distance ratio between the solution of the tactical model and that of the initial strategic model.

To understand the probabilities, we must first look at the drift, the value of the initial strategic model, then the probabilities.

For example:

• If the value of the initial [strategic model](./#the strategic-model) for a given output is 1000.
• And if, for period 1, we obtain a LowerProbability of 1 and a UpperProbability of 1 for a drift of 0.3.
  • Then this means that there is a 100% probability that the output will remain between a value of 700 and 1300 for period 1.
• And if, for period 10, we obtain a LowerProbability of 0.6 and a UpperProbability of 0.4 for a drift of 0.5.
  • This means that there is a 60% probability that the output will remain above 500, and a 40% probability that it will remain below 1500 in period 10.