Spatially referenced optimization
In the previous section, we’ve seen how to read a Woodstock model and load it into a FMTlpmodel object.
FMTlpmodel will allow you to solve a spatially referenced linear programming model, giving you an optimized schedule of forest operations according to a goal and a set of constraints.
Here, we will see how to do this optimization in practice.
A quick reminder of the meaning of “spatially referenced”
We can distinguish 3 ways that space can be taken into account in a model :
- In a non-spatial model or spatially implicit model, entities (e.g., forests, animals, agents, etc.) are not directly associated with a position in space, but the relation between them in the model can imply that only some of them interact with each other in a way to mimic a spatial disposition.
- In a spatially referenced model, entities are associated to regions in space, but not to a precise position in those regions; those regions can be non-continuous. Woodstock models are spatially referenced in nature, as they consider strata that correspond to forests with the same composition and age, which can be dispersed in many places in the landscape.
- In a spatially explicit model, entities are associated to precise coordinates in space, like in the pixels of a raster map.
The structure of the FMTlpmodel : FMTgraph and FMTdevelopment
FMTlpmodel, FMTgraph and FMTdevelopment are three classes that are important to understand how a linear programming model is represented in FMT, and how to solve it.
FMTlpmodel is a type III linear programming forest planning model, which is spatially referenced.
It can solve a type III forest planning model, and get an optimal harvest schedule using constraints and objectives defined by the user.
The FMTlpmodel contains an object called the FMTgraph, which contains the graph of the model. The graph is an ensemble of nodes linked together with vertices. Each node correspond to a possible state for a particular strata (which are spatially referenced groups of forest forest stands with the same characteristics), with each vertex representing a particular way that it can evolve to another state in the same period of time and between periods.
Here is a visual representation of a simple FMTgraph, in which a particular strata can evolve from different states (FMTdevelopment objects) with different transitions caused by different actions through the sme period of time. The evolution of the stands takes place between the periods and consists in increasing the age by 1 :
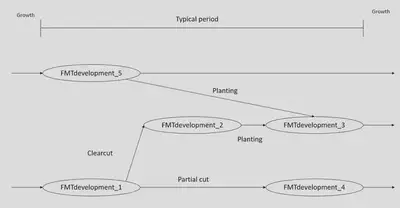
A FMTdevelopment is an important class of FMT. It represents a particular strata, which means a particular forest stand that has a given composition, age, and that exists at a particular time period.
Therefore, the FMTdevelopment object is associated with a FMTmask object, which described the set of attributes (FMTtheme) that defines the FMTdevelopment. This is shown on the following visual :
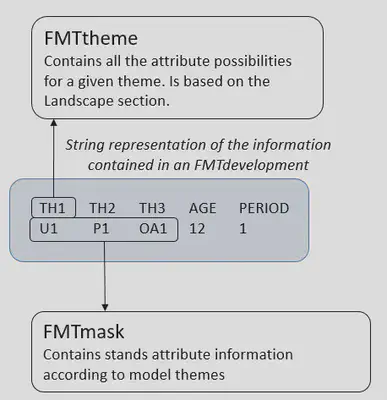
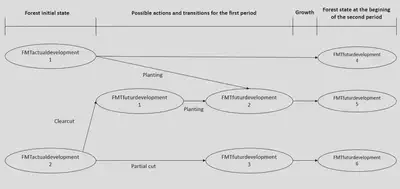
FMTdevelopment is the parent class of two classes, FMTactualdevelopment and FMTfuturdevelopment. An FMTactualdevelopment always represents a strata at the beginning of the planning horizon and therefore contains information about the area. The FMTfuturdevelopment are the possible futures and therefore no area is allocated to them when the FMTgraph is built. This is the result of the optimization that informs us about the future distribution of the area through the FMTgraph.
Here are some functions of the FMTdevelopment class that can be important for manipulating the model for different purposes :
FMTdevelopment.grow()can make the stand grow to see what it will become. Returns anFMTfuturdevelopmentidentical to theFMTdevelopmentfrom which the function is called but with an increased age of 1FMTdevelopment.operable()can test if a given action can be applied to this development, based on a yield section (e.g. a particular variable)FMTdevelopment.operate()can operate the stand, and return a vector ofFMTdevelopmentpath
Now, we can take a look at how to build the “full graph” of the model, which is necessary to solve the FMTlpmodel.
Building the full graph of the model
The full graph of the model can be built via a repetition of the function FMTlpmodel.buildperiod(). This is essential to solve the model, as FMT will navigate this graph to find the optimal solution according to the objective and the constraints that we will set (see next section).
This function requires three parameters :
- A schedule of actions, on the form of a
FMTscheduleobject (it can be empty to obtain the full graph for the model, containing every possibilities) - An option to force a partial build (which we will not see right now)
- Another parameter for class operability (that we will not see either right now, and just set to 1)
Here is the code to build the full graph in R. Pay attention to the to the for loop that builds the different periods.
library(FMT) # Loads FMT into R
if (new(FMTversion)$hasfeature("OSI")) # Checks if FMT has been compiled with OSI by creating a new FMTversion object, and using the function hasfeature().
{
# Creating the parser object to read the model files
newparser <- new(FMTmodelparser)
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist <- newmodelparser$readproject("Models/TWD_land/TWD_land.pri", c("LP"), TRUE, TRUE, TRUE)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
# We create an empty schedule to create the full graph
emptyschedule <- new(FMTschedule)
# We loop around the different periods to build the full graph
for (period in 1:10)
{
# We also want the prompt to display what is happening
print(lpmodel$buildperiod(emptyschedule,FALSE,1)$str())
}
} else { # if the model hasn't been compiled with OSI, we display an error.
print("FMT needs to be compiled with OSI")
}
The equivalent in Python code is the following (notice that in Python, we don’t have to make an empty schedule to build the full graph) :
import sys
from FMT import Models
from FMT import Parser
from FMT import Version
if __name__ == "__main__":
if Version.FMTversion().hasfeature("OSI"):
# Creating the parser object to read the model files
newmodelparser= Parser.FMTmodelparser()
path = "Models/TWD_Land/TWD_Land.pri"
scenarios = ["LP"]
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist = newmodelparser.readproject(path, scenarios)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
# We loop around the different periods to build the full graph
for period in range(1, 11):
print(lpmodel.buildperiod())
else:
print("FMT needs to be compiled with OSI")
The output of both codes should be the following :
Reading Models/TWD_land/TWD_land.pri
FMT 0.9.1, build: Sep 30 2021 12:07:49
Tue Oct 05 10:59:57 2021
Reading Scenario Lp
FMTexc(39)Undefined _death action: _DEATH FMTsection(4)Action
FMTexc(40)Undefined _death transition: _DEATH FMTsection(5)Transition
Done reading Tue Oct 05 10:59:57 2021
Columns: 58 Rows: 29 Vertices: 60 Edges: 58 Transfer Rows: 29 Output Rows: 0 Output Columns: 0
Columns: 169 Rows: 87 Vertices: 141 Edges: 169 Transfer Rows: 87 Output Rows: 0 Output Columns: 0
Columns: 336 Rows: 164 Vertices: 237 Edges: 336 Transfer Rows: 164 Output Rows: 0 Output Columns: 0
Columns: 553 Rows: 259 Vertices: 350 Edges: 553 Transfer Rows: 259 Output Rows: 0 Output Columns: 0
Columns: 805 Rows: 372 Vertices: 481 Edges: 805 Transfer Rows: 372 Output Rows: 0 Output Columns: 0
Columns: 1088 Rows: 503 Vertices: 630 Edges: 1088 Transfer Rows: 503 Output Rows: 0 Output Columns: 0
Columns: 1407 Rows: 652 Vertices: 797 Edges: 1407 Transfer Rows: 652 Output Rows: 0 Output Columns: 0
Columns: 1762 Rows: 819 Vertices: 982 Edges: 1762 Transfer Rows: 819 Output Rows: 0 Output Columns: 0
Columns: 2177 Rows: 1015 Vertices: 1196 Edges: 2177 Transfer Rows: 1015 Output Rows: 0 Output Columns: 0
Columns: 2660 Rows: 1244 Vertices: 1443 Edges: 2660 Transfer Rows: 1244 Output Rows: 0 Output Columns: 0
As we can see, the prompt shows us the evolutions of the characteristics of the FMTgraph as it gets built (increasing number of columns, vertices, etc.).
Constraints and objective
Linear programming models come with constraints and objectives, for which we want an optimized solution.
Hence, to solve a FMTlpmodel, we need to set these constraints and objectives into the model before attempting to solve it.
These constraints and objectives can be set manually via the FMTlpmodel.setobjective() and the FMTlpmodel.setconstraints() functions.
Most of the time, you might end up doing the following :
- Getting the constraints that are already in the Woodstock files formulation of the model using the
FMTmodel.getconstraint()function. - Taking out the first constraint out of the list of constraints that
FMTmodel.getconstraint()returns, because the first constraint of this list is actually the objective function of the model. - Then, inserting this objective function and the constraints into the
FMTlpmodelin order to solve it, by using theFMTlpmodel.setobjective()andFMTlpmodel.setconstraint()functions.
This will result in the following code, in R :
library(FMT) # Loads FMT into R
if (new(FMTversion)$hasfeature("OSI")) # Checks if FMT has been compiled with OSI by creating a new FMTversion object, and using the function hasfeature().
{
# Creating the parser object to read the model files
newparser <- new(FMTmodelparser)
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist <- newmodelparser$readproject("Models/TWD_land/TWD_land.pri", c("LP"), TRUE, TRUE, TRUE)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
# We create an empty schedule to create the full graph
emptyschedule <- new(FMTschedule)
# We loop around the different periods to build the full graph
for (period in 1:10)
{
# We also want the prompt to display what is happening
print(lpmodel$buildperiod(emptyschedule,FALSE,1)$str())
}
# We get the constraints and objectives
allmodelconstraints <- lpmodel$getconstraints()
# We define the first constraint of the list as the objective function of the model
modelobjective <- allmodelconstraints[[1]]
# We define all of the other constraints of the list as constraints
modelconstraints <- allmodelconstraints[2:length(allmodelconstraints)]
# We apply all of the constraints to the model
for (constraint in modelconstraints)
{
print(lpmodel$setconstraint(constraint)$str())
}
# We apply the objective function to the model
print(lpmodel$setobjective(modelobjective)$str())
} else { # if the model hasn't been compiled with OSI, we display an error.
print("FMT needs to be compiled with OSI")
}
The equivalent in Python code is the following (notice that here, we will just “take out” the objective function out of the list of constraints returned by FMTlpmodel.getconstraints() with the function list.pop(), which we allow us to directly loop around the remaining list for the constraints) :
import sys
from FMT import Models
from FMT import Parser
from FMT import Version
if __name__ == "__main__":
if Version.FMTversion().hasfeature("OSI"):
# Creating the parser object to read the model files
newmodelparser= Parser.FMTmodelparser()
path = "Models/TWD_Land/TWD_Land.pri"
scenarios = ["LP"]
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist = newmodelparser.readproject(path, scenarios)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
# We loop around the different periods to build the full graph
for period in range(1, 11):
print(lpmodel.buildperiod())
# We get the constraints and objectives
constraints = lpmodel.getconstraints()
# We define the first constraint of the list as the objective function of the model
objective = constraints.pop(0)
# We apply all of the constraints to the model
for constraint in constraints:
lpmodel.setconstraint(constraint)
# We apply the objective function to the model
lpmodel.setobjective(objective)
else:
print("FMT needs to be compiled with OSI")
Solving the FMTlpmodel
Once that the full graph is built, and that the constraints and objectives are set, the FMTlpmodel can be solved by using the FMTlpmodel.initialsolve() function. The function returns true or false depending on whether the model was successfully resolved. If the resolution went well, the model retains the solution and the solution can be queried in different ways (an example is shown below).
Building the graph with an existing solution (partial build)
Sometime, we might want to get some outputs of a solution/schedule that we already have (see next section) without solving the model all over again, as it was already solved previously.
In that case, it is possible to read a solution that was previously found, and to build the FMTgraph of the model by generating only the edges and vertices used by the solution.
To that end, three things must be done :
- Reading the schedule file of the scenario, and passing it to the
FMTlpmodel.buildperiod()function. - Setting the solution for each period with the
FMTlpmodel.setsolution()function- If the model contains multiple
_LOCKEXEMPTactions, then usingFMTlpmodel.setsolution()can throw errors as locks specifications are not part of the solution. In such a case, you should use theFMTlpmodel.setsolutionbylp()function.
- If the model contains multiple
This will result in the following code, in R :
library(FMT) # Loads FMT into R
if (new(FMTversion)$hasfeature("OSI")) # Checks if FMT has been compiled with OSI by creating a new FMTversion object, and using the function hasfeature().
{
# Creating the parser object to read the model files
newparser <- new(FMTmodelparser)
# Indicating where the model and the existing solution are
primarylocation <- "Models/TWD_land/TWD_land.pri"
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist <- newmodelparser$readproject(primarylocation, c("LP"), TRUE, TRUE, TRUE)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
# We read the existing schedule, which is the first of the list returned by the function
schedules <- newparser$readschedules(primarylocation,modelslist)[[1]]
# We create a "tolerance" variable that is needed for the setsolution function
tolerance <- 0.0001
# We loop around the different periods to build the partial graph with the existing solution
for (period in 1:length(schedules))
{
print(lpmodel$buildperiod(schedules[[period]],TRUE,1)$str())
}
# We set the solution of the model at each period
for (period in 1:length(schedules))
{
# We make an if statement to have an indication if FMT succeeded in applying the solution at this period
if (lpmodel$setsolution(period, schedules[[period]], tolerance))
{
print(paste("Solution set at period ", period))
}
}
} else { # if the model hasn't been compiled with OSI, we display an error.
print("FMT needs to be compiled with OSI")
}
Notice that here, we have a second parameter TRUE to lpmodel$buildperiod() to indicate that we needed to force a partial build, as indicated in the documentation of the function :

Also notice that we created a variable named tolerance, which is needed by the lpmodel$setsolution() function, as indicated by the documentation once again :

The equivalent in Python code is the following :
import sys
from FMT import Models
from FMT import Parser
from FMT import Version
if __name__ == "__main__":
if Version.FMTversion().hasfeature("OSI"):
# Creating the parser object to read the model files
newmodelparser= Parser.FMTmodelparser()
path = "Models/TWD_Land/TWD_Land.pri"
scenarios = ["LP"]
# Reading the project with the model parser by specifying that we want the scenario named "LP" (there can be different scenarios for one model)
modelslist = newmodelparser.readproject(path, scenarios)
# We cast the model in the "lpmodel" format for linear programming model by specifying the solver that we want to use
lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
# We create a "tolerance" variable that is needed for the setsolution function
tolerance = 0.0001
# We read the existing schedule, which is the first of the list returned by the function
schedules = newmodelparser.readschedules(path, modellist)[0]
# We loop around the different periods to build the partial graph with the existing solution
for periodschedule in range(len(schedules)):
print(lpmodel.buildperiod(schedules[periodschedule], False, 1))
# We set the solution of the model at each period (we use +1 as Python use a 0 based numbering)
for periodschedule in range(len(schedules)):
lpmodel.setsolution(periodschedule+1, schedules[periodschedule], tolerance)
print("Solution set at period", periodschedule+1)
else:
print("FMT needs to be compiled with OSI")
The output of both codes should be the following :
Reading Models/TWD_land/TWD_land.pri
FMT 0.9.1, build: Sep 30 2021 12:07:49
Tue Oct 05 10:59:57 2021
Reading Scenario Lp
FMTexc(39)Undefined _death action: _DEATH FMTsection(4)Action
FMTexc(40)Undefined _death transition: _DEATH FMTsection(5)Transition
Done reading Tue Oct 05 10:59:57 2021
Columns: 20 Rows: 10 Vertices: 28 Edges: 20 Transfer Rows: 10 Output Rows: 0 Output Columns: 0
Columns: 40 Rows: 25 Vertices: 48 Edges: 40 Transfer Rows: 25 Output Rows: 0 Output Columns: 0
Columns: 63 Rows: 44 Vertices: 71 Edges: 63 Transfer Rows: 44 Output Rows: 0 Output Columns: 0
Columns: 90 Rows: 67 Vertices: 98 Edges: 90 Transfer Rows: 67 Output Rows: 0 Output Columns: 0
Columns: 123 Rows: 95 Vertices: 131 Edges: 123 Transfer Rows: 95 Output Rows: 0 Output Columns: 0
Columns: 157 Rows: 126 Vertices: 165 Edges: 157 Transfer Rows: 126 Output Rows: 0 Output Columns: 0
Columns: 198 Rows: 162 Vertices: 206 Edges: 198 Transfer Rows: 162 Output Rows: 0 Output Columns: 0
Columns: 244 Rows: 203 Vertices: 252 Edges: 244 Transfer Rows: 203 Output Rows: 0 Output Columns: 0
Columns: 294 Rows: 248 Vertices: 301 Edges: 294 Transfer Rows: 248 Output Rows: 0 Output Columns: 0
Columns: 351 Rows: 298 Vertices: 356 Edges: 351 Transfer Rows: 298 Output Rows: 0 Output Columns: 0
Columns: 405 Rows: 350 Vertices: 410 Edges: 405 Transfer Rows: 350 Output Rows: 0 Output Columns: 0
Columns: 467 Rows: 407 Vertices: 472 Edges: 467 Transfer Rows: 407 Output Rows: 0 Output Columns: 0
Columns: 532 Rows: 468 Vertices: 537 Edges: 532 Transfer Rows: 468 Output Rows: 0 Output Columns: 0
Columns: 599 Rows: 532 Vertices: 604 Edges: 599 Transfer Rows: 532 Output Rows: 0 Output Columns: 0
Columns: 673 Rows: 601 Vertices: 678 Edges: 673 Transfer Rows: 601 Output Rows: 0 Output Columns: 0
Columns: 745 Rows: 671 Vertices: 749 Edges: 745 Transfer Rows: 671 Output Rows: 0 Output Columns: 0
Columns: 828 Rows: 747 Vertices: 831 Edges: 828 Transfer Rows: 747 Output Rows: 0 Output Columns: 0
Columns: 912 Rows: 827 Vertices: 915 Edges: 912 Transfer Rows: 827 Output Rows: 0 Output Columns: 0
Columns: 998 Rows: 910 Vertices: 1001 Edges: 998 Transfer Rows: 910 Output Rows: 0 Output Columns: 0
Columns: 1091 Rows: 998 Vertices: 1094 Edges: 1091 Transfer Rows: 998 Output Rows: 0 Output Columns: 0
Solution set at period 1
Solution set at period 2
Solution set at period 3
Solution set at period 4
Solution set at period 5
Solution set at period 6
Solution set at period 7
Solution set at period 8
Solution set at period 9
Solution set at period 10
Solution set at period 11
Solution set at period 12
Solution set at period 13
Solution set at period 14
Solution set at period 15
Solution set at period 16
Solution set at period 17
Solution set at period 18
Solution set at period 19
Solution set at period 20
Getting output values from the model
There are multiple ways to read different outputs from the model.
In R, there is a particular function (only available in R) called getoutsdataframe(); but for R, Python and C++, it is possible to use the FMTmodel.getoutputs() to get a list of the available outputs for a given model.
It is possible to select a different FMToutputlevel in order to obtain an output at different scales in the model.
For an example of this, see exercise 1.
Exporting the schedule of a solved model
Exporting the schedule of a solved model is done via the FMTscheduleparser object that we used when building the partial graph (see previous sections).
The solution of a model can be put into a list by using the FMTlpmodel.getsolution() function for each of the period of interest.
Then, the list of solution for each period must be transformed into a vector, which can then be written in a .txt file using the FMTscheduleparser.write() function.
For an example, see exercise 1.
Pre-solving a model
Some models can be hard to solve, because of their high number of actions, strata, and so on.
In such case, the FMTmodel.basepresolve() function can be used to pre-solve the model.
What this function does is to return a model with less themes, actions, transitions, outputs and constraints compare to the original model, but with the same amount of information. This makes it easier to solve, while giving the same answer in the end.
In some situations, FMT will pre-solve the model automatically.
Now that you know everything there is to know about spatially referenced optimization in FMT, we recommand that you try the exercise 1 to help you learn using FMT in practice. In this exercise, you will learn to use some of the most regularly used functions by yourself.