Optimisation spatiallement référencée

Dans la section précédente, nous avons vu comment lire un modèle Woodstock et le charger dans un objet FMTlpmodel.

FMTlpmodel vous permettra de résoudre un modèle de programmation linéaire à spatialement référencé, ce qui vous donnera un calendrier (schedule) optimisé d’opérations forestières en fonction d’un objectif et d’un ensemble de contraintes.

Ici, nous allons voir comment réaliser cette optimisation en pratique.

Un petit rappel sur la signification de “spatialement référencé”.

On peut distinguer 3 façons de prendre en compte l’espace dans un modèle :

• Dans un modèle non spatial ou modèle spatialement implicite, les entités (par exemple, les forêts, les animaux, les agents, etc.) ne sont pas directement associées à une position dans l’espace, mais la relation entre elles dans le modèle peut impliquer que seules certaines d’entre elles interagissent entre elles de manière à mimer une disposition spatiale.
• Dans un modèle spatialement référencé, les entités sont associées à des régions de l’espace, mais pas à une position précise dans ces régions ; ces régions peuvent être non-continues. Les modèles de Woodstock sont par nature spatialement référencés, car ils considèrent des strates qui correspondent à des forêts de même composition et de même âge, qui peuvent être dispersées en de nombreux endroits du paysage.
• Dans un modèle spatialement explicite, les entités sont associées à des coordonnées précises dans l’espace, comme dans les pixels d’une carte matricielle.

La structure du FMTlpmodel : FMTgraph et FMTdevelopment

FMTlpmodel, FMTgraph et FMTdevelopment sont trois classes qui sont importantes pour comprendre comment un modèle de programmation linéaire est représenté dans FMT, et comment le résoudre.

FMTlpmodel est un modèle de planification forestière à programmation linéaire de type III, qui est spatialement référencé.

Il peut résoudre un modèle de planification forestière de type III, et obtenir un calendrier de récolte optimal en utilisant les contraintes et les objectifs définis par l’utilisateur.

Le FMTlpmodel contient un objet appelé FMTgraph, qui contient le graphe du modèle. Le graphe est un ensemble de noeuds reliés entre eux par des liens. Chaque noeud correspond à un état possible pour une strate particulière (qui sont des groupes de peuplements forestiers référencés dans l’espace avec les mêmes caractéristiques), et chaque lien représente une façon particulière dont elle peut évoluer vers un autre état dans la même période de temps et entre les périodes.

Voici une représentation visuelle d’un FMTgraph simple, dans lequel une strate particulière peut évoluer à partir de différents états (objets FMTdevelopment) avec différentes transitions causées par différentes actions à travers la même période de temps. L’évolution des strates se fait entre les périodes et consiste à augmenter l’âge de ces dernières de 1 :

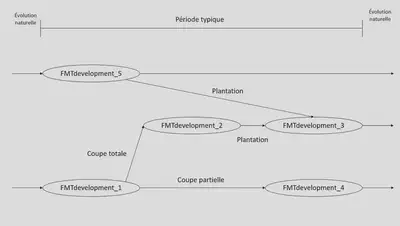
Un FMTdevelopment est une classe importante de FMT. Elle représente une strate particulière, c’est-à-dire un peuplement forestier particulier qui a une composition et un âge donnés, et qui existe à une période donnée.

Par conséquent, l’objet FMTdevelopment est associé à un objet FMTmask, qui décrit l’ensemble des attributs (FMTtheme) qui définit le FMTdevelopment. Ceci est illustré sur le visuel suivant :

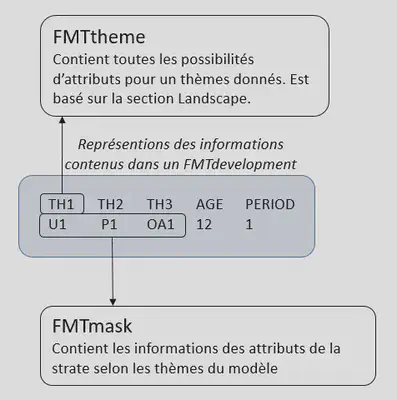
FMTdevelopment est la classe parente de deux classes, FMTactualdevelopment et FMTfuturdevelopment. Un FMTactualdevelopment représente toujours une strate en début d’horizon de planification et contient donc l’information de la superficie de la strate. Les FMTfuturdevelopment sont les futurs possibles et donc aucune superficie ne leur est attribuée au départ. C’est le résultat de l’optimisation qui nous informe sur la répartitions future des superficies au travers du FMTgraph.

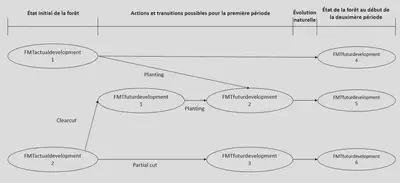
Voici ici quelques fonctions de la classe FMTdevelopment qui peuvent être importantes pour manipuler le modèle à différente fins :

• FMTdevelopment.grow() peut faire grandir le peuplement pour voir ce qu’il va devenir. Renvoie un FMTfuturdevelopment identique au FMTdevelopment à partir duquel la fonction est appelée mais avec un âge augmenté de 1
• FMTdevelopment.operable() peut tester si une action donnée peut être appliquée à ce développement, sur la base d’une section de yield(une variable particulière, par exemple)
• FMTdevelopment.operate() peut faire différentes actions sur la strate, et retourner un vecteur de FMTdevelopmentpath.

Maintenant, nous pouvons regarder comment construire le “graphe complet” du modèle, qui est nécessaire pour résoudre le FMTlpmodel.

Construire le graphe complet du modèle

Le graphe complet du modèle peut être construit via une répétition de la fonction FMTlpmodel.buildperiod(). Ceci est essentiel pour résoudre le modèle, car FMT va naviguer dans ce graphe pour trouver la solution optimale en fonction de l’objectif et des contraintes que nous allons fixer (voir section suivante).

Cette fonction nécessite trois paramètres :

• Un planning d’actions, sous la forme d’un objet FMTschedule (il peut être vide pour obtenir le graphe complet du modèle, contenant toutes les possibilités).
• Une option pour forcer une construction partielle du graphe (que nous ne verrons pas pour l’instant)
• Un autre paramètre pour l’opérabilité de la classe (que nous ne verrons pas non plus pour l’instant, et juste mis à 1)

Voici le code pour construire le graphe complet dans R. Notez la boucle for qui construit les différentes périodes.

library(FMT) # Charge FMT dans R
if (new(FMTversion)$hasfeature("OSI")) # Vérifie si FMT a été compilé avec OSI en créant un nouvel objet FMTversion, et en utilisant la fonction hasfeature().
{
	# Création de l'objet parser pour lire les fichiers de modèle
	newparser <- new(FMTmodelparser)
	# Lit le projet avec le parser en spécifiant que l'on veut lire le scénario "LP" (il peut y avoir différents scénarios dans un seul modèle)
	modelslist <- newmodelparser$readproject("Models/TWD_land/TWD_land.pri", c("LP"), TRUE, TRUE, TRUE)
	# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
	solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
	lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
	# Nous créons un calendrier vide pour créer le graphe complet
	emptyschedule <- new(FMTschedule)
	# On fait une boucle autour des différentes périodes pour construire le graphe complet
	for (period in 1:10)
	{
		# On affiche ce qui se passe dans le terminal
		print(lpmodel$buildperiod(emptyschedule,FALSE,1)$str())
	}
} else { # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur
	print("FMT needs to be compiled with OSI")
}

L’équivalent en code Python est le suivant (notez qu’en Python, nous n’avons pas besoin de faire un calendrier vide pour construire le graphique complet) :

import sys
from FMT import Models
from FMT import Parser
from FMT import Version

if __name__ == "__main__":
	if Version.FMTversion().hasfeature("OSI"):
		# Création de l'objet parser pour lire les fichiers de modèle
		newmodelparser=  Parser.FMTmodelparser()
		path = "Models/TWD_Land/TWD_Land.pri"
		scenarios = ["LP"]
		# Lit le projet avec le parser en spécifiant que l'on veut lire le scénario "LP" (il peut y avoir différents scénarios dans un seul modèle)
		modelslist = newmodelparser.readproject(path, scenarios)
		# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
		lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
		# On fait une boucle autour des différentes périodes pour construire le graphe complet
		for period in range(1, 11):
			print(lpmodel.buildperiod())
	else:
		print("FMT needs to be compiled with OSI") # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur

La sortie des deux codes devrait être la suivante :

Reading Models/TWD_land/TWD_land.pri
FMT 0.9.1, build: Sep 30 2021 12:07:49
Tue Oct 05 10:59:57 2021
Reading Scenario Lp
FMTexc(39)Undefined _death action: _DEATH FMTsection(4)Action
FMTexc(40)Undefined _death transition: _DEATH FMTsection(5)Transition
Done reading Tue Oct 05 10:59:57 2021
Columns: 58 Rows: 29 Vertices: 60 Edges: 58 Transfer Rows: 29 Output Rows: 0 Output Columns: 0
Columns: 169 Rows: 87 Vertices: 141 Edges: 169 Transfer Rows: 87 Output Rows: 0 Output Columns: 0
Columns: 336 Rows: 164 Vertices: 237 Edges: 336 Transfer Rows: 164 Output Rows: 0 Output Columns: 0
Columns: 553 Rows: 259 Vertices: 350 Edges: 553 Transfer Rows: 259 Output Rows: 0 Output Columns: 0
Columns: 805 Rows: 372 Vertices: 481 Edges: 805 Transfer Rows: 372 Output Rows: 0 Output Columns: 0
Columns: 1088 Rows: 503 Vertices: 630 Edges: 1088 Transfer Rows: 503 Output Rows: 0 Output Columns: 0
Columns: 1407 Rows: 652 Vertices: 797 Edges: 1407 Transfer Rows: 652 Output Rows: 0 Output Columns: 0
Columns: 1762 Rows: 819 Vertices: 982 Edges: 1762 Transfer Rows: 819 Output Rows: 0 Output Columns: 0
Columns: 2177 Rows: 1015 Vertices: 1196 Edges: 2177 Transfer Rows: 1015 Output Rows: 0 Output Columns: 0
Columns: 2660 Rows: 1244 Vertices: 1443 Edges: 2660 Transfer Rows: 1244 Output Rows: 0 Output Columns: 0

Comme on peut le voir, le terminal nous montre l’évolution des caractéristiques du FMTgraph au fur et à mesure de sa construction (nombre croissant de colonnes, de liens, etc.).

Contraintes et objectif

Les modèles de programmation linéaire sont accompagnés de contraintes et d’un objectif, pour lesquels nous voulons une solution optimisée.

Par conséquent, pour résoudre un FMTlpmodel, nous devons définir ces contraintes et objectifs dans le modèle avant de tenter de le résoudre.

Ces contraintes et objectifs peuvent être définis manuellement via les fonctions FMTlpmodel.setobjective() et FMTlpmodel.setconstraints().

La plupart du temps, vous allez finir par faire ce qui suit :

• Récupérer les contraintes qui sont déjà dans la formulation des fichiers Woodstock du modèle en utilisant la fonction FMTmodel.getconstraint().
• Retirer la première contrainte de la liste des contraintes que FMTmodel.getconstraint() renvoie, car la première contrainte de cette liste est en fait l’objectif du modèle.
• Ensuite, insérer cet objectif et les contraintes dans le FMTlpmodel afin de le résoudre, en utilisant les fonctions FMTlpmodel.setobjective() et FMTlpmodel.setconstraint().

Cela donnera le code suivant, dans R :

library(FMT) # Charge FMT dans R
if (new(FMTversion)$hasfeature("OSI")) # Vérifie si FMT a été compilé avec OSI en créant un nouvel objet FMTversion, et en utilisant la fonction hasfeature().
{
	# Création de l'objet parser pour lire les fichiers de modèle
	newparser <- new(FMTmodelparser)
	# Lit le projet avec le parser en spécifiant que l'on veut lire le scénario "LP" (il peut y avoir différents scénarios dans un seul modèle)
	modelslist <- newmodelparser$readproject("Models/TWD_land/TWD_land.pri", c("LP"), TRUE, TRUE, TRUE)
	# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
	solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
	lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
	# Nous créons un calendrier vide pour créer le graphe complet
	emptyschedule <- new(FMTschedule)
	# On fait une boucle autour des différentes périodes pour construire le graphe complet
	for (period in 1:10)
	{
		# On affiche ce qui se passe dans le terminal
		print(lpmodel$buildperiod(emptyschedule,FALSE,1)$str())
	}
	# On récupère les contraintes et objectifs
	allmodelconstraints <- lpmodel$getconstraints()
	# On définit la première contrainte de la liste comme l'objectif du modèle
	modelobjective <- allmodelconstraints[[1]]
	# On définit toutes les autres contraintes de la liste comme les contraintes du modèle
	modelconstraints <- allmodelconstraints[2:length(allmodelconstraints)]
	# On applique toutes les contraintes dans le modèle
	for (constraint in modelconstraints)
	{
		print(lpmodel$setconstraint(constraint)$str())
	}
	# On applique l'objectif au modèle
	print(lpmodel$setobjective(modelobjective)$str())
} else { # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur
	print("FMT needs to be compiled with OSI")
}

L’équivalent en code Python est le suivant (remarquez qu’ici, nous allons juste “sortir” la fonction objectif de la liste des contraintes retournée par FMTlpmodel.getconstraints() avec la fonction list.pop(), ce qui nous permet de boucler directement sur la liste restante pour les contraintes) :

import sys
from FMT import Models
from FMT import Parser
from FMT import Version

if __name__ == "__main__":
	if Version.FMTversion().hasfeature("OSI"):
		# Création de l'objet parser pour lire les fichiers de modèle
		newmodelparser=  Parser.FMTmodelparser()
		path = "Models/TWD_Land/TWD_Land.pri"
		scenarios = ["LP"]
		# Lit le projet avec le parser en spécifiant que l'on veut lire le scénario "LP" (il peut y avoir différents scénarios dans un seul modèle)
		modelslist = newmodelparser.readproject(path, scenarios)
		# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
		lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
		# On fait une boucle autour des différentes périodes pour construire le graphe complet
		for period in range(1, 11):
			print(lpmodel.buildperiod())
		# On récupère les contraintes et objectifs
		constraints = lpmodel.getconstraints()
		# On définit la première contrainte de la liste comme l'objectif du modèle
		objective = constraints.pop(0)
		# On applique toutes les contraintes dans le modèle
		for constraint in constraints:
			lpmodel.setconstraint(constraint)
		# On applique l'objectif au modèle
		lpmodel.setobjective(objective)
	else:
		print("FMT needs to be compiled with OSI") # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur

Résoudre le FMTlpmodel

Une fois que le graphe complet est construit, et que les contraintes et les objectifs sont fixés, le FMTlpmodel peut être résolu en utilisant la fonction FMTlpmodel.initialsolve(). La fonction renvoie une valeur true ou false selon que le modèle a été résolu avec succès. Si la résolution s’est bien passée, le modèle conserve la solution et cette dernière peut être interroger de différentes manières (un exemple est présenté plus bas).

Construire le graphe avec une solution existante (construction partielle)

Parfois, on peut vouloir obtenir des résultats d’une solution/planification que l’on a déjà déjà (voir la section suivante) sans résoudre le modèle à nouveau, puisqu’il a déjà été résolu précédemment.

Dans ce cas, il est possible de lire une solution qui a été trouvée précédemment, et de construire le FMTgraph du modèle en générant seulement les noeuds et les liens utilisés par la solution.

Pour cela, trois choses doivent être faites :

• Lire le fichier de calendrier du scénario, et le passer à la fonction FMTlpmodel.buildperiod().
• Définir la solution pour chaque période avec la fonction FMTlpmodel.setsolution().
  • Si le modèle contient plusieurs actions _LOCKEXEMPT, l’utilisation de FMTlpmodel.setsolution() peut provoquer des erreurs, car les verrous ne font pas partie de la solution. Dans ce cas, vous devez utiliser la fonction FMTlpmodel.setsolutionbylp().

Cela donnera le code suivant, dans R :

library(FMT) # Charge FMT dans R
if (new(FMTversion)$hasfeature("OSI")) # Vérifie si FMT a été compilé avec OSI en créant un nouvel objet FMTversion, et en utilisant la fonction hasfeature().
{
	# Création de l'objet parser pour lire les fichiers de modèle
	newparser <- new(FMTmodelparser)
	# Indique où le modèle et la solution existante se trouvent
	primarylocation <- "Models/TWD_land/TWD_land.pri"
	# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
	modelslist <- newmodelparser$readproject(primarylocation, c("LP"), TRUE, TRUE, TRUE)
	# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
	solverinterface <- list(CLP=1,MOSEK=2,CPLEX=3,GUROBI=4)
	lpmodel <- new(FMTlpmodel,modelslist[[1]],solverinterface$MOSEK)
	# On lit le calendrier existant, qui est le premier élément de la liste renvoyé par la fonction
	schedules <- newparser$readschedules(primarylocation,modelslist)[[1]]
	# On créer une variable "tolerance" qui est nécéssaire pour la fonction setsolution()
	tolerance <- 0.0001
	# On fait une boucle autour des périodes pour construire le graphe partiel avec la solution existante
	for (period in 1:length(schedules))
	{
		print(lpmodel$buildperiod(schedules[[period]],TRUE,1)$str())
	}
	# On definit la solution du modèle à chaque periode comme celle qui existait au depart
	for (period in 1:length(schedules))
	{
		# On fait en sorte que le terminal nous affiche quelque chose si la solution a bien été définie pour cette période
		if (lpmodel$setsolution(period, schedules[[period]], tolerance))
		{
			print(paste("Solution set at period ", period))
		}
	}
} else { # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur
	print("FMT needs to be compiled with OSI")
}

Remarquez qu’ici, on applique un deuxième paramètre TRUE à lpmodel$buildperiod() pour indiquer que nous voulons forcer une construction partielle, comme indiqué dans la documentation de la fonction :

Remarquez également que nous avons créé une variable nommée tolerance, qui est nécessaire à la fonction lpmodel$setsolution(), comme l’indique la documentation une fois de plus :

L’équivalent en code Python est le suivant :

import sys
from FMT import Models
from FMT import Parser
from FMT import Version

if __name__ == "__main__":
	if Version.FMTversion().hasfeature("OSI"):
		# Création de l'objet parser pour lire les fichiers de modèle
		newmodelparser=  Parser.FMTmodelparser()
		# Indique où le modèle et la solution existante se trouvent
		path = "Models/TWD_Land/TWD_Land.pri"
		scenarios = ["LP"]
		# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
		modelslist = newmodelparser.readproject(path, scenarios)
		# On met le modèle dans le format "lpmodel" pour le modèle de programmation linéaire, en spécifiant le solveur que nous voulons utiliser
		lpmodel = Models.FMTlpmodel(modelslist[0], Models.FMTsolverinterface.CLP)
		# On créer une variable "tolerance" qui est nécéssaire pour la fonction setsolution()
		tolerance = 0.0001
		# On lit le calendrier existant, qui est le premier élément de la liste renvoyé par la fonction
		schedules = newmodelparser.readschedules(path, modellist)[0]
		# On fait une boucle autour des périodes pour construire le graphe partiel avec la solution existante
		for periodschedule in range(len(schedules)):
			print(lpmodel.buildperiod(schedules[periodschedule], False, 1))
		# On definit la solution du modèle à chaque periode comme celle qui existait au depart (on utilise +1 pour s'adapter au fait que Python commence ses listes à 0)
		for periodschedule in range(len(schedules)):
			lpmodel.setsolution(periodschedule+1, schedules[periodschedule], tolerance)
			print("Solution set at period", periodschedule+1) 
	else:
		print("FMT needs to be compiled with OSI") # Si le modèle n'as pas été compilé avec OSI, on affiche une erreur

La sortie des deux codes devrait être la suivante :

Reading Models/TWD_land/TWD_land.pri
FMT 0.9.1, build: Sep 30 2021 12:07:49
Tue Oct 05 10:59:57 2021
Reading Scenario Lp
FMTexc(39)Undefined _death action: _DEATH FMTsection(4)Action
FMTexc(40)Undefined _death transition: _DEATH FMTsection(5)Transition
Done reading Tue Oct 05 10:59:57 2021
Columns: 20 Rows: 10 Vertices: 28 Edges: 20 Transfer Rows: 10 Output Rows: 0 Output Columns: 0
Columns: 40 Rows: 25 Vertices: 48 Edges: 40 Transfer Rows: 25 Output Rows: 0 Output Columns: 0
Columns: 63 Rows: 44 Vertices: 71 Edges: 63 Transfer Rows: 44 Output Rows: 0 Output Columns: 0
Columns: 90 Rows: 67 Vertices: 98 Edges: 90 Transfer Rows: 67 Output Rows: 0 Output Columns: 0
Columns: 123 Rows: 95 Vertices: 131 Edges: 123 Transfer Rows: 95 Output Rows: 0 Output Columns: 0
Columns: 157 Rows: 126 Vertices: 165 Edges: 157 Transfer Rows: 126 Output Rows: 0 Output Columns: 0
Columns: 198 Rows: 162 Vertices: 206 Edges: 198 Transfer Rows: 162 Output Rows: 0 Output Columns: 0
Columns: 244 Rows: 203 Vertices: 252 Edges: 244 Transfer Rows: 203 Output Rows: 0 Output Columns: 0
Columns: 294 Rows: 248 Vertices: 301 Edges: 294 Transfer Rows: 248 Output Rows: 0 Output Columns: 0
Columns: 351 Rows: 298 Vertices: 356 Edges: 351 Transfer Rows: 298 Output Rows: 0 Output Columns: 0
Columns: 405 Rows: 350 Vertices: 410 Edges: 405 Transfer Rows: 350 Output Rows: 0 Output Columns: 0
Columns: 467 Rows: 407 Vertices: 472 Edges: 467 Transfer Rows: 407 Output Rows: 0 Output Columns: 0
Columns: 532 Rows: 468 Vertices: 537 Edges: 532 Transfer Rows: 468 Output Rows: 0 Output Columns: 0
Columns: 599 Rows: 532 Vertices: 604 Edges: 599 Transfer Rows: 532 Output Rows: 0 Output Columns: 0
Columns: 673 Rows: 601 Vertices: 678 Edges: 673 Transfer Rows: 601 Output Rows: 0 Output Columns: 0
Columns: 745 Rows: 671 Vertices: 749 Edges: 745 Transfer Rows: 671 Output Rows: 0 Output Columns: 0
Columns: 828 Rows: 747 Vertices: 831 Edges: 828 Transfer Rows: 747 Output Rows: 0 Output Columns: 0
Columns: 912 Rows: 827 Vertices: 915 Edges: 912 Transfer Rows: 827 Output Rows: 0 Output Columns: 0
Columns: 998 Rows: 910 Vertices: 1001 Edges: 998 Transfer Rows: 910 Output Rows: 0 Output Columns: 0
Columns: 1091 Rows: 998 Vertices: 1094 Edges: 1091 Transfer Rows: 998 Output Rows: 0 Output Columns: 0
Solution set at period   1
Solution set at period   2
Solution set at period   3
Solution set at period   4
Solution set at period   5
Solution set at period   6
Solution set at period   7
Solution set at period   8
Solution set at period   9
Solution set at period   10
Solution set at period   11
Solution set at period   12
Solution set at period   13
Solution set at period   14
Solution set at period   15
Solution set at period   16
Solution set at period   17
Solution set at period   18
Solution set at period   19
Solution set at period   20

Obtenir des valeurs de sortie du modèle

Il existe plusieurs façons de lire les différentes sorties du modèle.

En R, il existe une fonction particulière (seulement disponible en R) appelée getoutsdataframe() ; mais pour R, Python et C++, il est possible d’utiliser la fonction FMTmodel.getoutputs() pour obtenir une liste des sorties (outputs) disponibles pour un modèle donné.

Il est possible de sélectionner un FMToutputlevel différent afin d’obtenir une sortie à différentes échelles dans le modèle.

Pour un exemple, voir exercice 1.

Exportation du calendrier d’un modèle résolu

L’exportation du calendrier d’un modèle résolu se fait via l’objet FMTscheduleparser que nous avons utilisé lors de la construction du graphe partiel (voir sections précédentes).

La solution d’un modèle peut être mise dans une liste en utilisant la fonction FMTlpmodel.getsolution() pour chacune des périodes d’intérêt.

Ensuite, la liste des solutions pour chaque période doit être transformée en un vecteur, qui peut ensuite être écrit dans un fichier .txt en utilisant la fonction FMTscheduleparser.write().

Pour un exemple, voir exercice 1.

Présolution d’un modèle

Certains modèles peuvent être difficiles à résoudre, à cause de leur nombre élevé d’actions, de strates, et ainsi de suite.

Dans ce cas, la fonction FMTmodel.basepresolve() peut être utilisée pour présolutioner le modèle.

Cette fonction retourne un modèle avec moins de thèmes, d’actions, de transitions, de sorties et de contraintes que le modèle original, mais avec la même quantité d’informations. Cela le rend plus facile à résoudre, tout en donnant la même réponse à la fin.

Dans certaines situations, FMT présolutionerra le modèle automatiquement.

Maintenant que vous savez tout ce qu’il y a à savoir sur l’optimisation à spatialement référencée dans FMT, nous vous recommandons d’essayer l’exercice 1 pour vous aider à apprendre à utiliser FMT en pratique. Dans cet exercice, vous apprendrez à utiliser par vous-même certaines des fonctions les plus régulièrement utilisées.